1530. 好叶子节点对的数量 #

Difficulty: 中等

给你二叉树的根节点 root 和一个整数 distance 。

如果二叉树中两个叶节点之间的 最短路径长度 小于或者等于 distance ，那它们就可以构成一组 好叶子节点对 。

返回树中 好叶子节点对的数量 。

示例 1：

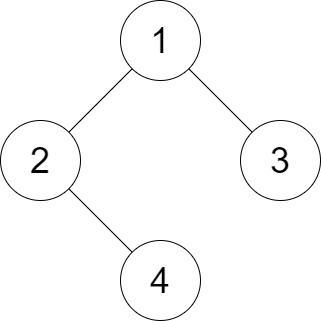
输入：root = [1,2,3,null,4], distance = 3
输出：1
解释：树的叶节点是 3 和 4 ，它们之间的最短路径的长度是 3 。这是唯一的好叶子节点对。

示例 2：

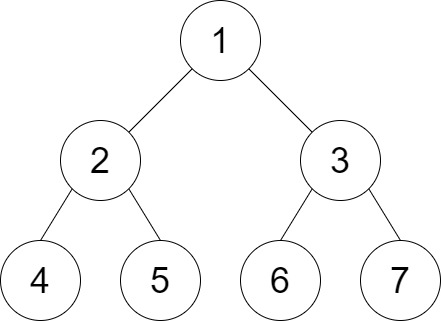
输入：root = [1,2,3,4,5,6,7], distance = 3
输出：2
解释：好叶子节点对为 [4,5] 和 [6,7] ，最短路径长度都是 2 。但是叶子节点对 [4,6] 不满足要求，因为它们之间的最短路径长度为 4 。

示例 3：

输入：root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3
输出：1
解释：唯一的好叶子节点对是 [2,5] 。

示例 4：

输入：root = [100], distance = 1
输出：0

示例 5：

输入：root = [1,1,1], distance = 2
输出：1

提示：

tree 的节点数在 [1, 2^10] 范围内。
每个节点的值都在 [1, 100] 之间。
1 <= distance <= 10

题解 #

解法一：递归解法 #

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int countPairs(TreeNode root, int distance) {
        Pair pair = dfs(root, distance);
        return pair.count;
    }

    // 对于 dfs(root,distance)，同时返回：
    // 1）每个叶子节点与 root 之间的距离
    // 2) 以 root 为根节点的子树中好叶子节点对的数量
    public Pair dfs(TreeNode root, int distance) {
        int[] depths = new int[distance + 1];
        boolean isLeaf = root.left == null && root.right == null;
        if (isLeaf) { 
            depths[0] = 1;
            return new Pair(depths, 0);
        }

        int[] leftDepths = new int[distance + 1];
        int[] rightDepths = new int[distance + 1];
        int leftCount = 0, rightCount = 0;
        if (root.left != null) {
            Pair leftPair = dfs(root.left, distance);
            leftDepths = leftPair.depths;
            leftCount = leftPair.count;
        }
        if (root.right != null) {
            Pair rightPair = dfs(root.right, distance);
            rightDepths = rightPair.depths;
            rightCount = rightPair.count;
        }

        for (int i = 0; i < distance; i++) {
            depths[i + 1] += leftDepths[i];
            depths[i + 1] += rightDepths[i];
        }

        int cnt = 0;
        for (int i = 0; i <= distance; i++) {
            for (int j = 0; j + i + 2 <= distance; j++) {
                cnt += leftDepths[i] * rightDepths[j];
            }
        }
        return new Pair(depths, cnt + leftCount + rightCount);
    }
}

class Pair {
    int[] depths;
    int count;

    public Pair(int[] depths, int count) {
        this.depths = depths;
        this.count = count;
    }
}